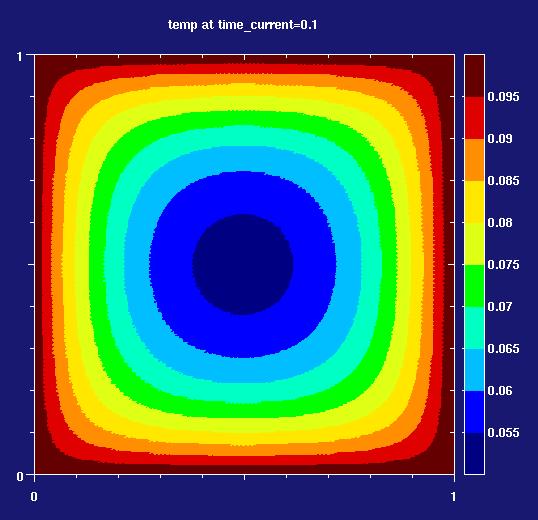
This example shows the application of the iterative linear equations solver for a large computation. The solver is a Preconditioned BiConjugate Gradient solver (PBCG). The solver is applied to a two-dimensional temperature field.
A rectangular plate is heated from the edges. Heat capacity is present, so the temperatures inside the plate follow the temperature on the edges only slowly. In the calculations, the setup of the element matrices and the PBCG solver run in parallel. The cpu times required with a different amount of finite elements, linear quadrilateral elements with four integrations points each, are given below. The error in the linear equations is required to be lower then 1.e-6 times the initial error in the linear equations. The calculation has been done on a sgi o200 workstation with 2 Mips 185 MhZ R10000 processors.
| number of elements | cpu time for mesh generation | cpu time for setup of matrices and PBCG solver | cpu time for total calculation |
| 10 thousand | 0.1 min. | 0.5 min. | 0.6 min. |
| 40 thousand | 0.3 min | 3.4 min. | 3.7 min. |
| 90 thousand | 0.7 min. | 10.8 min. | 11.5 min. |
| 160 thousand | 1.3 min. | 24.7 min. | 26.0 min. |
| 250 thousand | 2.4 min. | 46.0 min. | 48.4 min. |
Finally we show the temperature field for the analysis with 10,000 elements, to get a better impression of the physical problem. The amount of elements, 250 thousand elements for the largest mesh, is not required for accuracy, by only meant to demonstrate the behavior of the solver.

Here is the Inputfile.