Example 2: Confined compression of fluid filled porous material

In this 1D example, a porous solid saturated with fluid is compressed by a force $F$ on the solid phase. The length of the test specimen is $L$, plane strain conditions hold, the Young's modulus is $E$, Poisson's ratio is $\nu$, permeability $k_p$, width of test specimen $W$, thickness $T$, area $A=WT$. Some non-dimensional variables are introduced

$$X = x/L \; \; \; \; \; T = \frac{Hk_p}{L^2} t \; \; \; \; \; P = \frac{Ap}{F}$$

$$H=\frac{E(1-\nu)}{(1+\nu)(1-2\nu)}$$

At $X=1$ free drainage holds ($P=0$) for $T>0$. At $X=0$ the boundary is not permeable ( $\frac{\partial P}{\partial X} = 0$) for $T>0$. Using the non-dimensional variables, the analytical solution reads (see [1])

$$P = \sum_{n=0}^{\infty} \frac{2}{M} \sin(MX) \exp (-M^2T)$$

$$M = \frac{\pi}{2} (2n+1)$$

As a typical result, $P$ at $T=0.22$ is checked; at $X=0.4$ the exact solution for the non-dimensional pressure $P$ is 0.6.

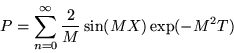
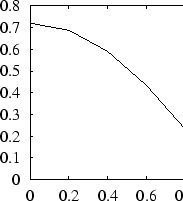
Now we choose: $L=1$, $W=1$, $T=1$, $E=1.e1$, $\nu=0$, $k_p=0.1$ and $F=1$. Thus, for $x=0.4$ at $t=0.22$ we should find $p=0.6$. The numerical analysis (5 elements, time step size 0.01) gives $p=0.607$. The pressure distribution at $T=0.22$ is given below