


Next: Example 5: Inverse modeling
Up: Examples
Previous: Example 3: Plasticity in
Contents
This example demonstrates the effect of the spatial stabilization algorithm
in 2D.
A convection and diffusion of heat equation is analyzed on
a 1 by 1 square.
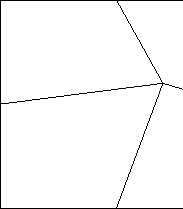
The two-dimensional mesh consists of distorted linear quadrilaterals
The convection velocity 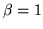 and the conductivity
and the conductivity 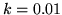 .
The boundary conditions for temperature are chosen such that the exact
solution for a boundary layer in
.
The boundary conditions for temperature are chosen such that the exact
solution for a boundary layer in 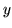 -direction holds:
-direction holds:
where we choose 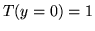 and
and 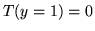 .
This is a severe test for the spatial stabilization algorithm.
Many algorithms exist which solve this example exactly when
using a one-dimensional domain, say with
.
This is a severe test for the spatial stabilization algorithm.
Many algorithms exist which solve this example exactly when
using a one-dimensional domain, say with 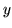 -axis only, but few exist
which do not show wiggles for irregular 2D grids.
The node_dof records are initialized
with temperature 1 as a first estimate for the solution field.
The we check the results at
-axis only, but few exist
which do not show wiggles for irregular 2D grids.
The node_dof records are initialized
with temperature 1 as a first estimate for the solution field.
The we check the results at 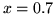 and
and 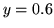 .
The exact solution is 1.
The numerical solution with the 4-noded elements is 0.95.
Splitting the elements in triangles
(see control_mesh_split) would have given the solution 1.001.
Triangles seem to behave better than distorted quads (in this example anyway).
Both solutions are quite good however.
.
The exact solution is 1.
The numerical solution with the 4-noded elements is 0.95.
Splitting the elements in triangles
(see control_mesh_split) would have given the solution 1.001.
Triangles seem to behave better than distorted quads (in this example anyway).
Both solutions are quite good however.



Next: Example 5: Inverse modeling
Up: Examples
Previous: Example 3: Plasticity in
Contents
tochnog
2001-09-02

![]() and the conductivity
and the conductivity ![]() .
The boundary conditions for temperature are chosen such that the exact
solution for a boundary layer in
.
The boundary conditions for temperature are chosen such that the exact
solution for a boundary layer in ![]() -direction holds:
-direction holds: