Example 7: Global mesh refinement over polynomial domain

This example shows that mesh refinement follows the boundaries of a domain; more precisely, if the nodes of an element edge are all placed on a specific geometrical entity (geometry_line, geometry_circle, etc.) then new generated nodes along that edge will also be placed on that geometrical entity; see refine_globally_geometry for this. Here we mesh a domain bounded at the left and right side by vertical lines ($x=0$ and $x=10$), bounded at the bottom by the polynomial $y = -10 - 10x + x^2$ and bounded at the top by the polynomial $y = +10 + x^2 - 0.1x^3$. Initially only one 4-noded quadrilateral is used

The four nodes of the element are placed on the intersection points of the polynomials and the lines. After 4 global refinements the mesh looks like

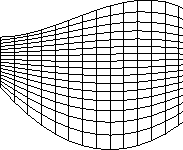
Each refinement is accompanied by some remeshing in order to obtain a more regular mesh.