next up previous contents
Next: Example 12: Contact frictional Up: Examples Previous: Example 10: Shear of   Contents

Example 11: Propagation of a disturbance in the wave equation.

The wave equation is used over a one-dimensional domain (between $x=0$ and $x=1$). The domain is divided into 128 linear elements. At time $t=0$, $s=0$ over the entire domain. After time $t=0$, at $x=0$ the scalar $s$ is prescribed to hold the value $0$ and at $x=1$ the rate of the scalar s ($\dots $) is prescribed to have the value $1. \; 10 ^{-4}$. This disturbance at the right edge propagates into the domain with the speed of sound ($c=1$). At time $0.5$ the rate of $s$ over the entire domain is monitored; at this time point $\dots $ should have become $1. \; 10 ^{-4}$ in the right half of the domain, whereas nothing should have happened yet in the left half of the domain. 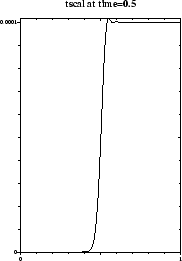The first plot shows $\dots $ if we use purely explicit time stepping (control_timestep_iterations is set to 1).

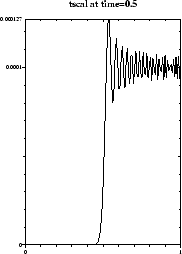
\begin{figure}\centerline{\epsfig{file=ps/ex111.ps,width=4cm}}\end{figure}

It is clear that the disturbance did propagate into half of the domain, but quite some oscillations do show up. The oscillations are greatly reduced if two iterations are used (control_timestep_iterations is set to 2); see the second plot.

\begin{figure}\centerline{\epsfig{file=ps/ex112.ps,width=4cm}}\end{figure}

next up previous contents
Next: Example 12: Contact frictional Up: Examples Previous: Example 10: Shear of   Contents
tochnog 2001-09-02